1. Newton's Life
Isaac Newton was born on Christmas day 1642 in a Lincolnshire manor house.
Newton was named after his recently deceased father (a wealthy farmer) and raised by his maternal grandmother after his mother remarried.
Education and early work
He did well at school despite or perhaps because of being bullied, and entered Trinity College, Cambridge, in 1661.
Newton graduated in 1665, the same year as he discovered the binomial mathematical theory, and returned to his childhood home of Woolsthorpe Manor in Lincolnshire—when the university was closed because of an outbreak of plague—to develop his theories on optics, mechanics, the law of gravitation and calculus.
It was during this period that Newton developed his laws of motion. Newton later described these years as the "prime" of his "age for invention".
Principia Mathematica and Opticks
Newton returned to Cambridge, as a fellow of Trinity College, two years later. He was promoted to be the Lucasian Professor of Mathematics in 1669, probably as a result of his invention of the reflecting telescope (which brought him to the attention of the scientific establishment) the previous year.
Newton, however, refused to take holy orders, as was required by the University’s bylaws, and Charles II granted him a special dispensation.
Newton’s greatest work, Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), was published in 1687. His second most influential book, Opticks, followed in 1704.
Alchemy and later life
In addition to physics and mathematics, Newton devoted time to alchemy (and in particular the transformation of base metals to gold) and biblical chronology (the study of the order of events described in the Old Testament). Newton's attempts at alchemy probably contributed to his 1693 nervous breakdown; he became obsessed with this endeavour and often worked through the night.
Newton held a number of other important roles, devoting his later years to legislative or administrative positions: he was twice elected the member of parliament for Cambridge University; he was appointed warden of the Royal Mint in 1696; he was elected president of the Royal Society in 1703; and he was knighted in 1705.
Newton died in 1727 and was buried in Westminster Abbey.
Did Newton die a virgin?
Newton's most productive period took place before he was 30 years old, and he was lucky enough to have been recognised as a genius in his own lifetime. But he never married and some maintain that he died a virgin.
At least one eminent psychologist believes that Newton suffered from Aspergers syndrome. He was certainly a workaholic, an insomniac and a bit of a nutter: he once stared at the sun for so long that he had to spend three days in a darkened room to let his eyes recover.
2. Mechanics and Gravity
In Principea, Newton set out his three laws of motion.
The first is the law of inertia: objects at rest stay at rest, and objects in motion stay in motion at the same speed, unless acted upon by an external force.
The second is the law of acceleration, which is equal to the force applied on a body divided by its mass. These two laws were groundbreaking: since Aristotle, received wisdom had been that a force was necessary in order to maintain motion.
The third law provides that for every action there must be an equal and opposite reaction. So, when a marksman pulls the trigger on his rifle, the force of the bullet is equal to the recoil into his shoulder.
Universal gravitation
These three laws go hand-in-hand with Newton’s law of universal gravitation. This law states that any two bodies in the universe attract each other with a force directly proportionate to the product of their masses and inversely proportionate to the square of the distance between them.
It is this theory that explained why an apple falls to the ground from a tree (the earth’s mass attracts it) and why the moon orbits the earth (again, the earth’s mass attracts it).
It is also this theory that explains the earth’s orbit around the sun (it is held in orbit by the sun’s mass)—a conclusion that finally silenced those who continued to doubt that the sun is the centre of our solar system.
A falling apple?
Legend has it that Newton's theory of universal gravitation was inspired by watching a falling apple in his Lincolnshire garden. Evidence emerged in 2010, in the form of a diary kept by Newton's friend William Stukeley, to suggest that the story is true.
3. Mathematics
In the field of mathematics, Newton and a German mathematician called Gottfried Leibniz are credited with the invention of infinitesimal calculus (the study of change).
There was a bitter dispute between the two men (and indeed English and German scientists more generally) as to which scholar should take credit, with allegations and counter-allegations of plagiarism made.
The truth is that both men arrived at their conclusions independently and had a different emphasis: Newton was the first to apply calculus to physics and Leibniz developed much of the notation used today.
Newton made a number of other mathematical discoveries, contributing to the power series, generalizing the binomial theorem and developing a method for approximating the roots of a function.
4. Optics and legacy
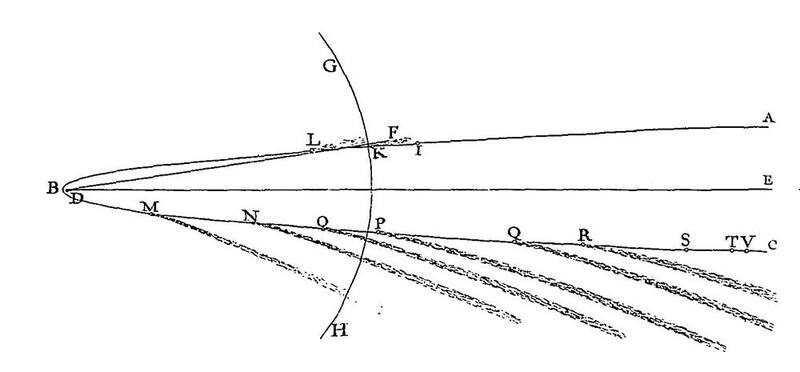
In this field, Newton studied the works of English physicists Robert Boyle and Robert Hooke and experimented extensively by refracting light through a glass prism.
He derived two profound conclusions:
- that white light is a mixture of rays of the whole spectrum of coloured light (as seen in the rainbow); and
- that light is a stream of minute particles.
Whilst these theories were first conceived in the late 1660s, they were not fully described by Newton until the publication of Opticks in 1704.
This was because Newton’s inchoate ideas had been the subject of hostile criticism—his detractors, the Dutch physicist Christiaan Huygens in particular, thought that colours were modified forms of white light.
Some say that Newton waited for his critics to die before he published Opticks.
Newton ranks ahead of the nation's other leading scientists, including names such as Charles Darwin, Alexander Flemming, Boyle, Watson and Crick, Professor Willmot and Tim Berners-Lee.